코드만 급하신 분
#분산분석
result=aov(종속변수~독립변수,전체데이터)
#p값 확인
summary(result)일원분산분석이란?
분산분석은 3개 이상의 그룹의 평균을 비교할 때 사용하는 검정방법입니다. 독립변수와 종속변수의 수에 따라 아래와 같이 나뉩니다.
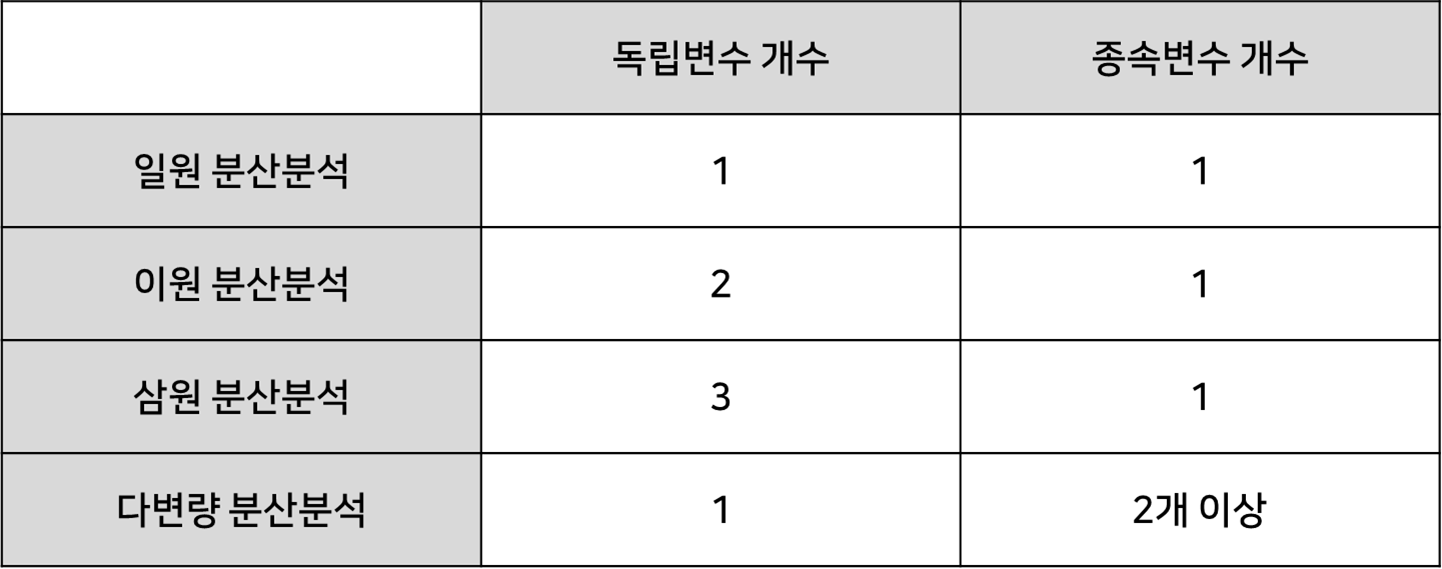
이번글에서 다루는 일원분산분석은 독립변수가 1개이고 종속변수도 1개인 경우입니다. 예를 들면 '세 반의 수학점수 평균 비교' 가 있습니다. 이 때 독립변수는 반의 종류이고 종속변수는 수학점수입니다.
일원분산분석의 귀무가설과 대립가설은 아래와 같습니다.
귀무가설 : 세 집단의 평균이 같다.
대립가설 : 적어도 어느 한 모집단은 다른 모집단과 평균이 다르다.
일원 분산분석의 조건
일원분산분석은 세가지 조건을 만족해야 합니다.
1) 독립성
2) 정규성
3) 등분산성
집단 사이에 독립성을 만족하지 않고 대응되어 있는 경우 '반복측정 분산분석'을 사용합니다. 각 집단이 정규성을 만족하지 않는 경우 Kruskal-Wallis test 를 사용합니다. 집단 사이에 등분산성을 만족하지 않는 경우 Welch 의 강건한 분산분석을 합니다. 세 집단 이상의 등분산 검정은 barlett.test 를 통해 수행합니다.
예제
1) 데이터 전처리
A반, B반, C반의 수학점수를 비교해 볼 것입니다. 수학점수는 아래와 같습니다. 총 30명인데,10명만 표시했습니다.
데이터 엑셀 파일은 아래와 같습니다.
데이터를 R에서 열어봅시다. 코드는 아래와 같습니다.
library(readxl)
md <- read_excel("파일경로/1way_ANOVA_R.xlsx")
md=as.data.frame(md)
View 함수로 열어보면 아래와 같습니다.
View(md)

위 데이터에서 독립변수와 종속변수를 구분해봅시다. 독립변수는 '반'이고, 종속변수는 '점수'입니다. 데이터를 R에서 사용하려면 아래와 같은 형태로 바꿔주어야 합니다.
위와 같이 바꾸는 코드는 아래와 같습니다.
#각 반의 데이터를 독립변수, 종속변수 형태로 만들어줌
classA=data.frame(rep("A",length(md$A)),md$A)
classB=data.frame(rep("B",length(md$B)),md$B)
classC=data.frame(rep("C",length(md$C)),md$C)
#열 이름을 통일해줌
colnames(classA)=c("x","y")
colnames(classB)=c("x","y")
colnames(classC)=c("x","y")
#세 반의 데이터를 행 방향으로 합쳐줌
md2=rbind(classA,classB,classC)
View 함수로 다시 열어보면 아래와 같습니다.
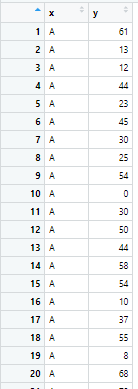
변경이 잘 되었습니다.
2) 분산분석
분산분석에는 aov 함수가 사용됩니다. 사용 형식은 아래와 같습니다.
aov(종속변수~독립변수,데이터)
위 데이터에 적용하면 아래와 같습니다.
> aov(y~x,md2)
Call:
aov(formula = y ~ x, data = md2)
Terms:
x Residuals
Sum of Squares 9677.4 33218.6
Deg. of Freedom 2 87
Residual standard error: 19.54029
Estimated effects may be unbalanced
p값을 출력하는 방법은 아래와 같습니다. summary 함수를 이용합니다.
> summary(aov(y~x,md2))
Df Sum Sq Mean Sq F value Pr(>F)
x 2 9677 4839 12.67 1.48e-05 ***
Residuals 87 33219 382
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
p값이 0.05보다 작으므로, 유의차가 있습니다. 하지만 ANOVA 만으로는 어느 그룹간의 유의차가 있는지를 알 수 없습니다. 적어도 두 그룹 모집단의 평균이 서로 다르다는 것만 알 수 있습니다.
어느 그룹간에 유의차가 있는지는 '사후분석'을 통해 알 수 있습니다.
3) 사후분석
사후분석은 여러 종류가 있습니다.
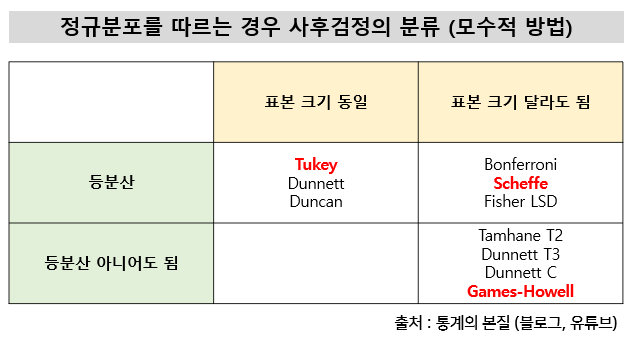
가장 많이 사용되는 쉐페(Scheffe) 방법을 사용 해봅시다. 먼저 라이브러리를 설치하고 불러옵니다. 먼저 라이브러리를 설치하고 불러옵니다.
install.packages("DescTools")
library(DescTools)
분산분석 결과를 저장합니다.
my_aov=aov(y~x,md2)
Scheffe 검정은 아래와 같이 수행합니다.
> ScheffeTest(my_aov)
Posthoc multiple comparisons of means: Scheffe Test
95% family-wise confidence level
$x
diff lwr.ci upr.ci pval
B-A 14.6 2.034725 27.16527 0.0184 *
C-A 25.3 12.734725 37.86527 1.6e-05 ***
C-B 10.7 -1.865275 23.26527 0.1116
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
A와 B 사이에는 차이가 있고, A와 C 사이에도 차이가 있는 것으로 나옵니다.
#전체 코드
library(readxl)
md <- read_excel("경로/1way_ANOVA_R.xlsx")
#각 반의 데이터를 독립변수, 종속변수 형태로 만들어줌
classA=data.frame(rep("A",length(md$A)),md$A)
classB=data.frame(rep("B",length(md$B)),md$B)
classC=data.frame(rep("C",length(md$C)),md$C)
#열 이름을 통일해줌
colnames(classA)=c("x","y")
colnames(classB)=c("x","y")
colnames(classC)=c("x","y")
#세 반의 데이터를 행 방향으로 합쳐줌
md2=rbind(classA,classB,classC)
#ANOVA
my_aov=aov(y~x,md2)
summary(my_aov) #p-value
#scheffe test
library(DescTools)
ScheffeTest(my_aov)

댓글